So the limit as x approaches infinity of f of x is the limit as x approaches infinity of 10 over 12 over x Now this piece goes to 0 so this limit is 10 over 10 or 10 Let's try this trick and the limit as x approaches negative infinity Now we can still use the fact that f of x equals 10 over 12 over x, so the limit as x approaches negativeLet us approximate the value of the limit lim x→1 √x 3 − 2 x − 1 Step 1 Go to "Y=", then type in the function Step 2 Go to "TBL SET" (2ndWINDOW), then set TblStart=97 and Δ Tbl=01 (Note TblStart is the starting xvalue in the table, so put a number slightly smaller that the number x approaches Δ Tbl is the increment valueWe now have a lot of experience taking limits of functions if I'm taking the limit of f of X what we're gonna think about what is FX approach as X approaches some value a and this would be equal to some limit now everything we've done up till now is where a is a finite value but when you look at the graph of the function f right over here you see something interesting happens as X gets

Limits At Infinity Infinite Limits And Asymptotes
Lim x approaches infinity f(x)=0 graph
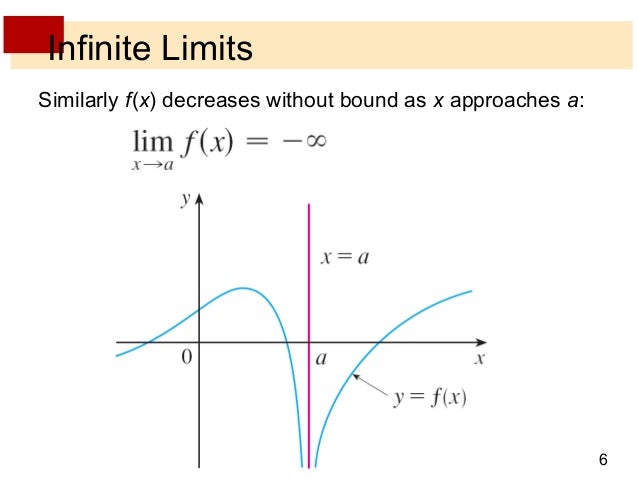
Lim x approaches infinity f(x)=0 graph-How to show the limit of (1x)^(1/x) is equal to the constant 'e'Begin by letting a variable equal to the limit, then apply the natural logarithm to both sidIt says that the limit of the function as X approaches for is equal to negative infinity That means the limit of the function as exit purchase for on both the positive and negative sides equals negative infinity So in order to draw this, we can draw this graph where the graph slowly approaches negative affinity as it gets closer and closer to




Why Is Limit Of This Function Infinity As X Approaches Infinity Mathematics Stack Exchange
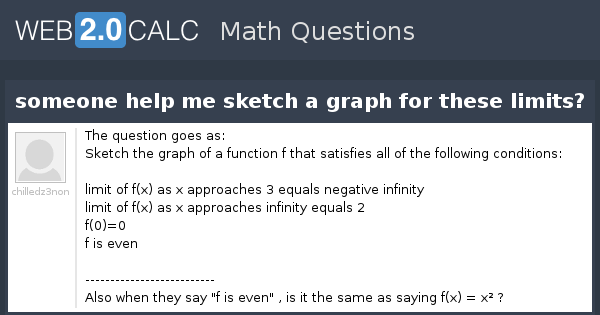
Sketch the graph of a function f that satisfies the given values f(0) is undefined lim x > 0 f(x) = 4 f(2) = 6 lim x > 2 f(x) = 3 Solution From the given question, We understood that the functions is undefined when x = 0 When the value of x approaches 0 from left hand side and right hand side, limit value will approaches to 4Move the x slider so that x gets bigger and bigger As you will note, f (x) approaches 0 for this example We write In this case, we can also say that , because the function also approaches 0 as you head towards negative infinity Select the second example In this example, the limit at positive infinity is different from the limit at negative infinity Select the third example This is just a line10 For the same function as in #9, what is its limit as x approaches 2?
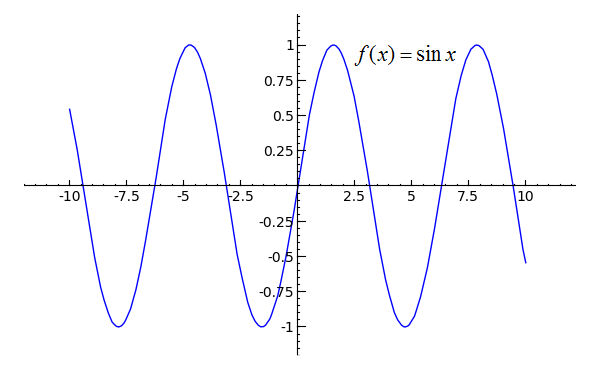
Explanation You're going to want to use the squeeze theorem for this Recall that sinx is only defined on −1 ≤ sinx ≤ 1 Therefore And since lim x→∞ − 1 x = lim x→ ∞ 1 x = 0, then lim x→∞ sinx x = 0 Hopefully this helps!What is its derivative at xWhat is its limit as x approaches negative infinity?
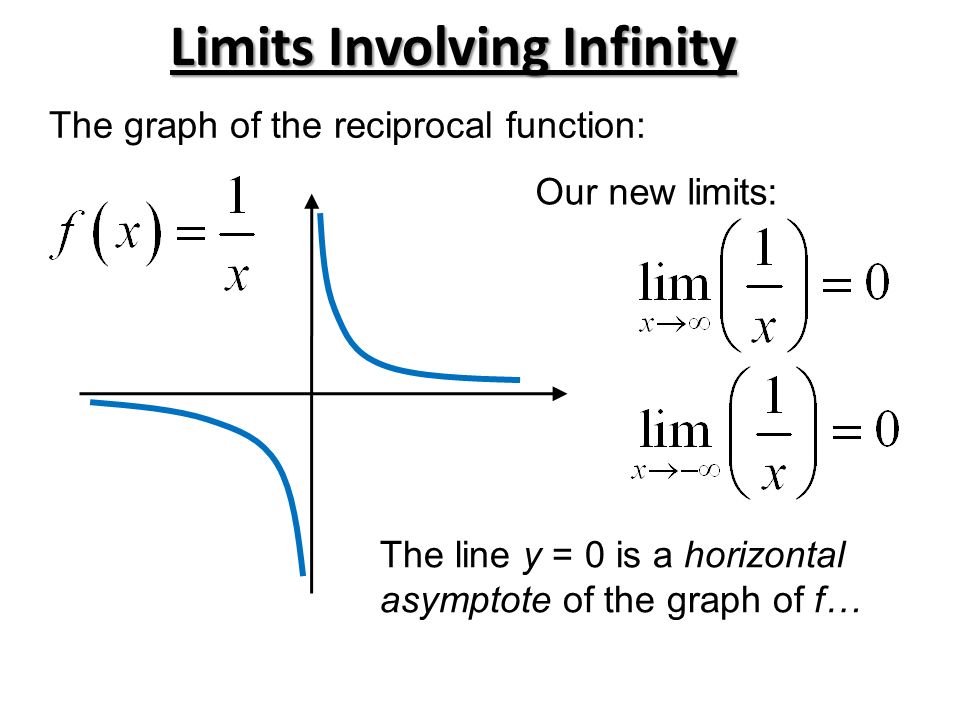
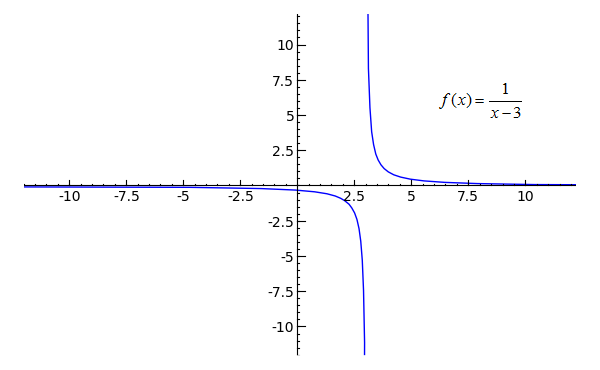
A function has a limit at infinity (or negative infinity) if it approaches a horizontal asymptote In particular, the graph of f(x)= 1 xn f (x) = 1 x n (with n > 0 n > 0) has a horizontal asymptote at y = 0, y = 0, so lim x→∞f(x)= 0 = lim x→−∞f(x) lim x → ∞ f (x) = 0 = lim x → − ∞ f (x) Clearly, if we take larger and larger values of x, the value of the fraction becomes smaller and smaller until it gets very close to `0` We say that "the limit of `5/x` as x approaches infinity is `0`" We write this in mathematical notation as `lim_(x>oo)(5/x)=0`What we're going to do in this video is use the online graphing calculator desmos and explore the relationship between vertical and horizontal asymptotes and think about how they relate to what we know about limits so let's first graph 2 over X minus 1 so let me get that one graphed and so you can immediately see that something interesting happens at X is equal to 1 if you were to just



Lecture 6 Limits With Infinity



Calculus Limit Function Take The Limit As X Approaches
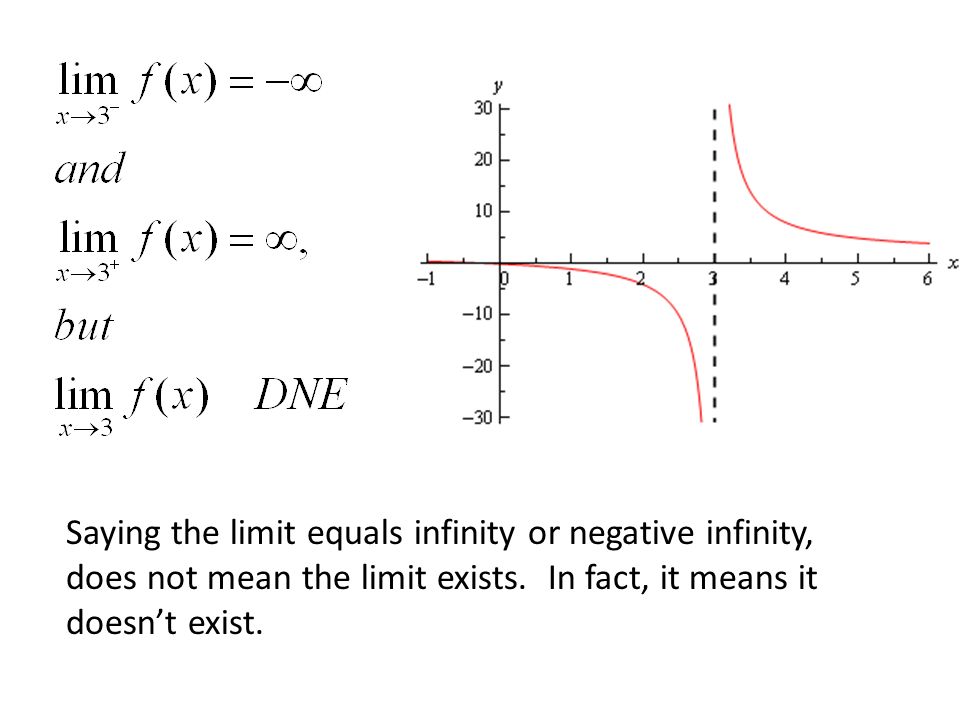
$$ \lim\limits_{x\to\infty} f(x) \approx 8 $$ When Limits at Infinity Don't Exist In order for a limit at infinity to exist, the function must approach a particular finite valueThe limit of an oscillating function f(x) as x approaches positive or negative infinity is undefined In the plot that you just created, try replacing 'sin' with various other trigonometric functions such as 'cos', 'tan', 'sec', 'csc', 'cot', or any of the arcfunctions (like 'arctan') to observe whether they oscillate or whether they have a horizontal asymptote as x approaches positive or negative infinityThe limit of f(x) as x approaches 2 from the left does not equal f(2), however, so f(x) is not continuous from the left at 2 Onesided limits are usually fairly straightforward However, be aware that when a function approaches a vertical asymptote , such as at x=0 in the following graph, you would describe the limit of the function as approaching oo or oo, depending on the case




How To Find Limit Of Functions As X Approaches Infinity Youtube




Limits
Please be sure to answer the questionProvide details and share your research!It#appearsthat,#asx#getscloser#and#closer#to#2#from# theleft,f(x)#getscloser#and#closer#to#05# Wesaythat*thelimit*of*f(x),*as*x*approaches*2*from*the left,*equals*05* * € x→2− limf(x)=05% Thisvalueisalsocalled"theleftFhand*limitas%x% approaches2"% It#also#appearsthat,#asx#getscloser#and#closer#to#2# from#the#right,#f(x)#getscloser#and#closer#to#0About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators



View Question Someone Help Me Sketch A Graph For These Limits




2 6 Limits At Infinity X X As X Approaches Infinity F X As X Gets Larger And Larger F X As X Gets Larger And Larger In The Negative Direction Ppt Download
lim x→∞ x −cosx x = lim x→∞ x x − cosx x = lim x→∞ 1 − cosx x = lim x→∞ 1 − lim x→∞ cosx x → lim x→∞ cosx x = 0 The range of cosx is −1 ≤ cosx ≤ 1, however as x → ∞ you are dividing a small number by an increasingly large number Thus = 1 − 0 = 1 Answer link Peter MI'm unsure if it approaches $0$ or if it's nonexistent Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careersThere is no finite number that you can plug into 1/x to give zero If you think about it as an algebraic expression ( y = 1/x ), plug 0 in for y and try to solve for x 0 = 1/x (multiply both sides by x) 0*x = 1 We know that this cannot happen, as 0 times anything is 0



Http Www Utm Utoronto Ca Asc Sites Files Asc Public Shared Pdf Tip Sheets Math Rgasc Cmath Limits as x approaches infinity 1117 Pdf



L Hopital S Rule Wikipedia
Calculus Limits Limits at Infinity and Horizontal Asymptotes 1 AnswerBut avoid Asking for help, clarification, or responding to other answers Explanation Notice that (1 4 x)x = exln(1 4 x) and if the limit exists, lim x→∞ (exln(1 4 x)) = e lim x→∞ (xln(1 4 x)) as the exponential function is continuous everywhere To evaluate the limit at the exponent, we first write it as xln(1 4 x) = ln(1 4 x) 1 x Since the form is indeterminate 0 0, use the L'hospital rule




Find Lim F X As X Approaches 0 If It Exists Study Com



Section 2 2a Limits Involving Infinity We Can Say The Limit Of F As X Approaches Infinity Meaning The Limit Of F As X Moves Increasingly Far To The Ppt Download
Limit at Infinity (Formal Definition) If f is a function, we say that lim x → ∞f(x) = L if for every ϵ > 0 there is an N > 0 so that whenever x > N, f(x) − L < ϵ We may similarly define lim x → − ∞f(x) = L 🔗 We include this definition for completeness, but we will not explore it in detailLim x → ( π / 2) tan x = − ∞, it follows that lim x → − ∞ tan − 1 ( x) = − π 2 As a result, y = π 2 and y = − π 2 are horizontal asymptotes of f ( x) = tan − 1 ( x) as shown in the following graph Figure 7 This function has two horizontal asymptotes Evaluate lim x → − ∞(3 4 x) and lim x → ∞(3 4 x)Sketch a graph of a function f (x) that has the following properties lim as x approaches infinity is f (x)= infinity lim as x approaches 6 from the left is f (x) infinity and lim as x approaches 6 from the right is f (x)= infinity lim as x approaches 3 is f (x)= 5 f (3)=6 f (0)=1 f' (0)=0 f''




Limit Of A Function Wikipedia



Week 3 Limits Involving Infinity And Continuity Ap Calculus
There are instances where the limit of f (x) f(x) f (x) as x x x approaches x 0 x_0 x 0 increases or decreases without bound In such cases, it is often said that the limit exists and the value is infinity (or negative infinity) However, some resources say that the limit does not exist in this instance, simply because this restriction makes other theorems in calculus slightly easier to state and Therefore, $\sin(\infty)$, which makes sense by the fact that as x approaches 0, the input of sine will increase to infinity or some large number As a What is the limit of #xe^(1/x) x# as x approaches infinity?




Functions Graphs And Limits Horizontal Asymptoes



Sage Calculus Tutorial Limits At Infinity
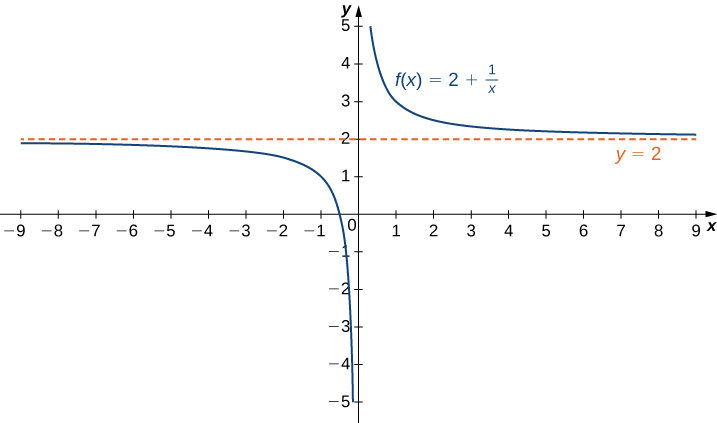
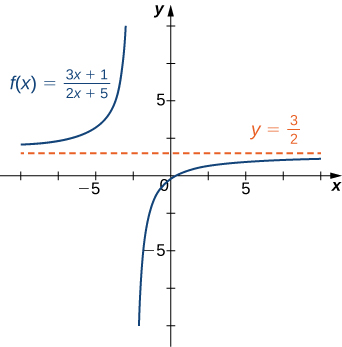
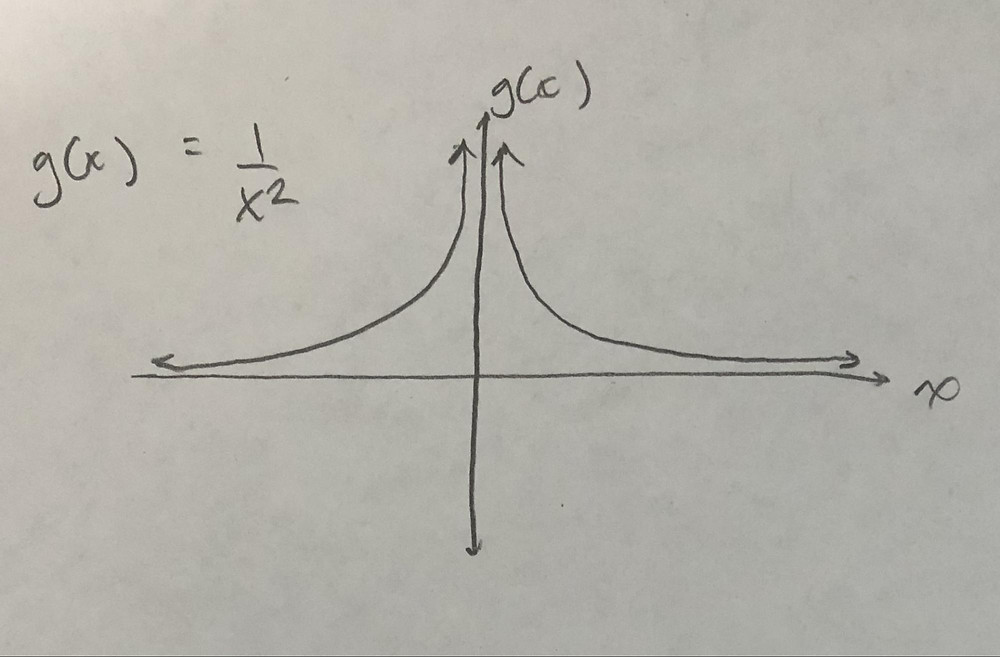
It seems appropriate, and descriptive, to state that lim x → 0 1 x2 = ∞ Also note that as x gets very large, f(x) gets very, very small We could represent this concept with notation such as lim x → ∞ 1 x2 = 0 FIGURE 130 Graphing f(x) = 1 / x2 for values of x near 0 We explore both types of use of ∞ in turnSo we have f of X equaling 4x to the fifth minus 3x squared plus 3 all of that over 6x to the fifth minus 100x squared minus 10 and what I want to think about is what is the limit of f of X as X approaches as X approaches infinity and there are several ways that you could do this you could actually try to plug in larger and larger numbers for X and see if it seems to be approaching some As can be seen graphically in Figure and numerically in Table, as the values of x get larger, the values of f(x) approach 2 We say the limit as x approaches ∞ of f(x) is 2 and write lim x → ∞ f(x) = 2 Similarly, for x < 0, as the values x get larger, the values of f(x) approaches 2



Limits Involving Infinity Section 1 4 Infinite Limits A Limit In Which F X Increases Or Decreases Without Bound As X Approaches C Is Called An Infinite Ppt Download



Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora
3 Sqrt(9∞^41)~~3∞^2(1/6)*0² Please note that 1/infinity is infinitesimal and won't be noticed on a graph 3∞^2/(∞^2–3∞5) Divide both sides of the equation by infinity squared 1/infinity will be treated as zero 1 is nothing compared to infiLimits at Infinity Consider the graph of the function f ( x) = 1 e x shown below Clearly, looking at the graph, the height of this function appears to get closer and closer to a height of zero, as we look at x values farther and farther to the right That is to say, it appears that f ( x) → 0 as x → ∞ In other functions, such as fWhat is its limit as x approaches 0?
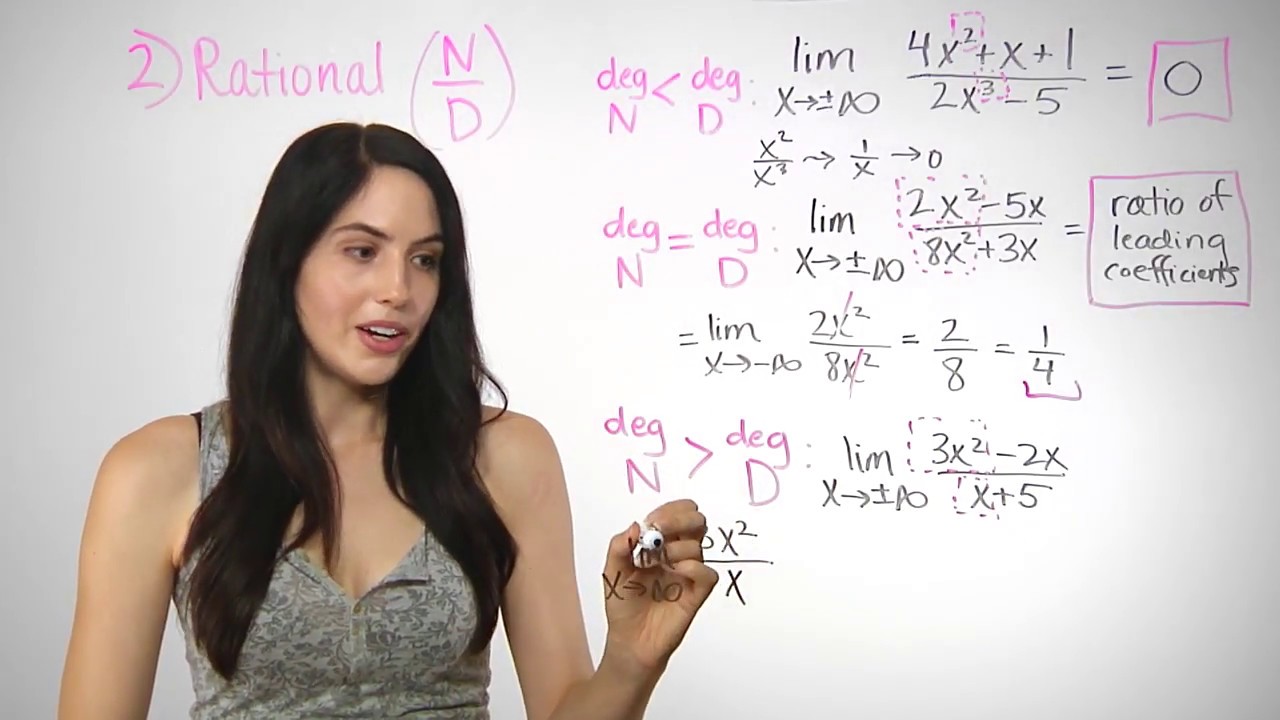



How To Find The Limit At Infinity Nancypi Youtube



Sage Calculus Tutorial Limits At Infinity
Here is what I mean The expression x →∞ just means x increases forThe graph of f (x) = ln (x) f (x) = ln (x) is the reflection of the graph of y = e x y = e x about the line y = x y = x Therefore, ln (x) → − ∞ ln (x) → − ∞ as x → 0 x → 0 and ln (x) → ∞ ln (x) → ∞ as x → ∞ x → ∞ as shown in Figure 461 and Table 46When students first meet concepts like this they really need explanations in simple language which is not full of mathematical terms that only make sense to other mathematicians!
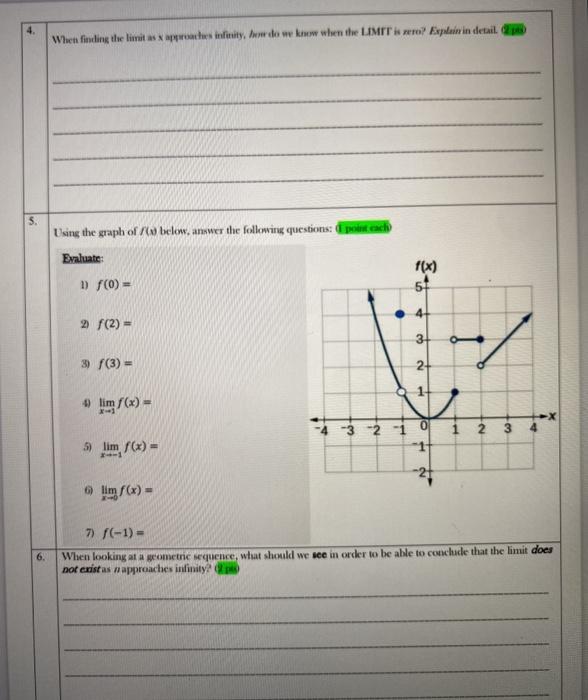



When Finding The Limits X Approaches Infinity How Do Chegg Com
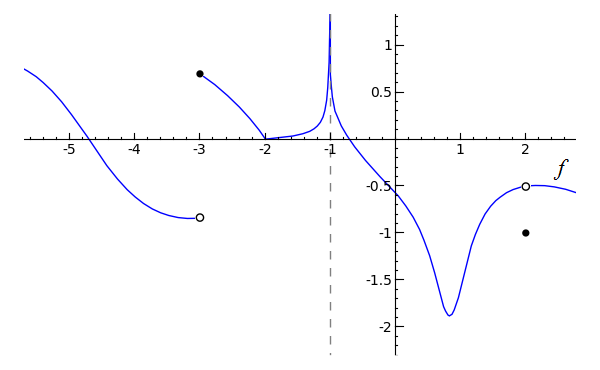



Sage Calculus Tutorial One Sided Limits
Limit as x approaches infinity of cosx,tanx, cotx, secx, cscx DNE The negative side of the graph ( asymptote at X=0 ) the limit as X approaches c of f(x) exists ( limit from the left of c equals the limit from the right of c) 2) f(c) exists ( a solid point) lim x → ∞ − 1 x = 0 = lim x → ∞ 1 x, we can apply the squeeze theorem to conclude that lim x → ∞ sinx x = 0 Similarly, lim x → − ∞ sinx x = 0 Thus, f(x) = sinx x has a horizontal asymptote of y = 0 and f(x) approaches this horizontal asymptote as x → ± ∞ as shown in the following graphLim x → ∞ f(x) = 0 lim x → ∞ f(x) = 0 An example with a function that has a limit of two at infinity For the function in the graph below, we first consider the behavior of f(x) as as x increases without bound, or in other words, we consider what happens to f(x) as we move farther and farther to the right on the graph




The Squeeze Theorem




7 Determine The Domain Of F X 1x And Graph The Chegg Com
For example, the limit of the following graph is 0 as x approaches infinity, clearly seen as the graph approaches 0 like so Now, let's look at a few examples where we can find the limit of real functions Example A Find the limit of \(f(x) = 4x\), as x approaches 3 Steps 1) Replace x The limit as x approaches zero would be negative infinity, since the graph goes down forever as you approach zero from either side As a general rule , when you are taking a limit and the denominator equals zero, the limit will go to infinity or negative infinity (depending on the sign of the function) In that case, we write lim x → ∞ f(x) = L Similarly, we say the limit as x → − ∞ of f(x) is L if f(x) becomes arbitrarily close to L as long as x < 0 and x is sufficiently large In that case, we write lim x → − ∞ f(x) = L We now look at the definition of a function having a limit at infinity




Calculus How To Find Limits With Infinity Using The Graph Youtube
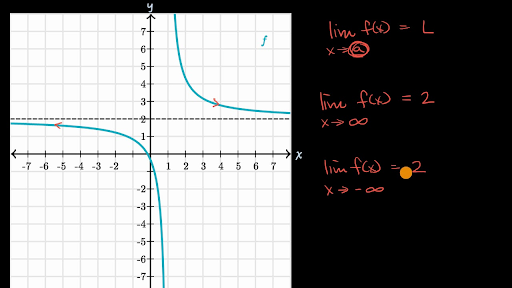



Introduction To Limits At Infinity Video Khan Academy
Limits at Infinity and Horizontal Asymptotes Recall that means becomes arbitrarily close to as long as is sufficiently close to We can extend this idea to limits at infinity For example, consider the function As can be seen graphically in and numerically in , as the values of get larger, the values of approach 2 We say the limit as approaches of is 2 and write Similarly, for as the As can be seen graphically in Figure 141 and numerically in Table 141, as the values of x get larger, the values of f(x) approach 2 We say the limit as x approaches ∞ of f(x) is 2 and write lim x → ∞ f(x) = 2 Similarly, for x < 0, as the values x get larger, the values of f(x) approachesRule 1 The limit as x approaches 0 from the left must equal the limit as x approaches 0 from the right This rule is broken As we can see a "jump" when we look at the graph, the limit from the left will not equal the limit from the right The limit as x approaches 0 from the left is 1, while the limit as x approaches 0 from the right is 0



Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora
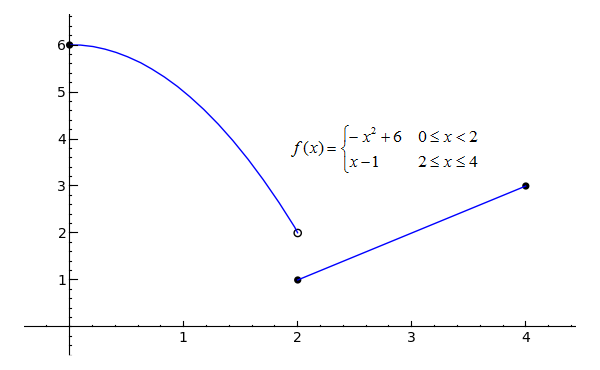



Sage Calculus Tutorial One Sided Limits
If $$\lim_{x\to a}f(x)=\infty$$, is it always true, that $$ \lim_{x\to a} f'(x) \ge0 $$ if the limit exists (or is infin Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Thanks for contributing an answer to Mathematics Stack Exchange!Smaller, the values of f (x) become larger and larger No matter what big number we call, you can appoint a value of x such that the value of f (x) will be larger than that number we have appointed We therefore say that the values of f (x) become or tend to infinity Let's say that as x approaches 0, the limit of f (x) is the infinite
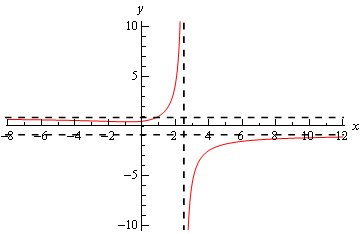



Calculus I Limits At Infinity Part I
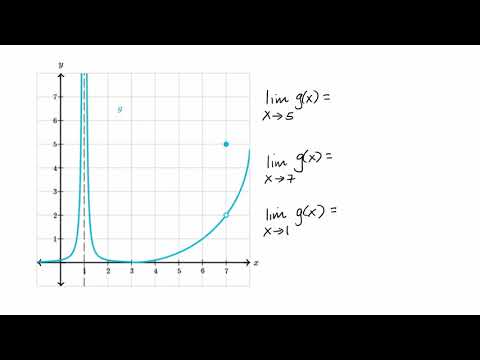



Estimating Limit Values From Graphs Video Khan Academy
Transcribed image text sinx, when x < 0 1 when 05x2 x > 2 9 Graph the function f(x) = 3 x, when What is its limit as x approaches positive infinity?Free Limit at Infinity calculator solve limits at infinity stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy




Limits To Infinity




2 6 Limits At Infinity X X As X Approaches Infinity F X As X Gets Larger And Larger F X As X Gets Larger And Larger In The Negative Direction Ppt Download
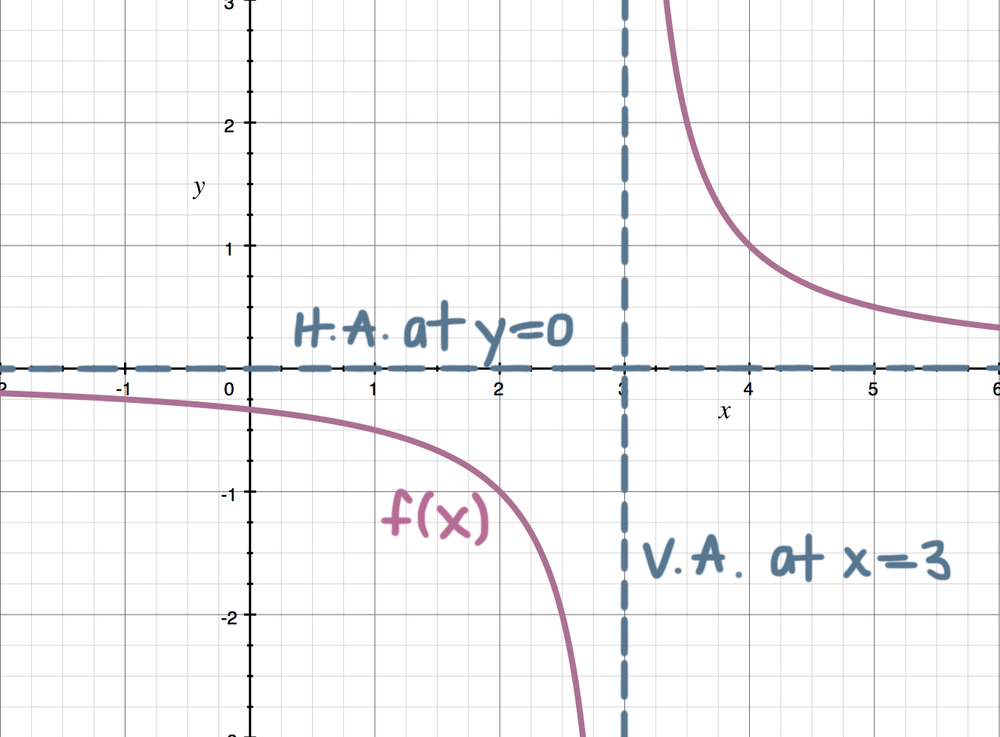



Limits At Infinity And Horizontal Asymptotes Krista King Math Online Math Tutor
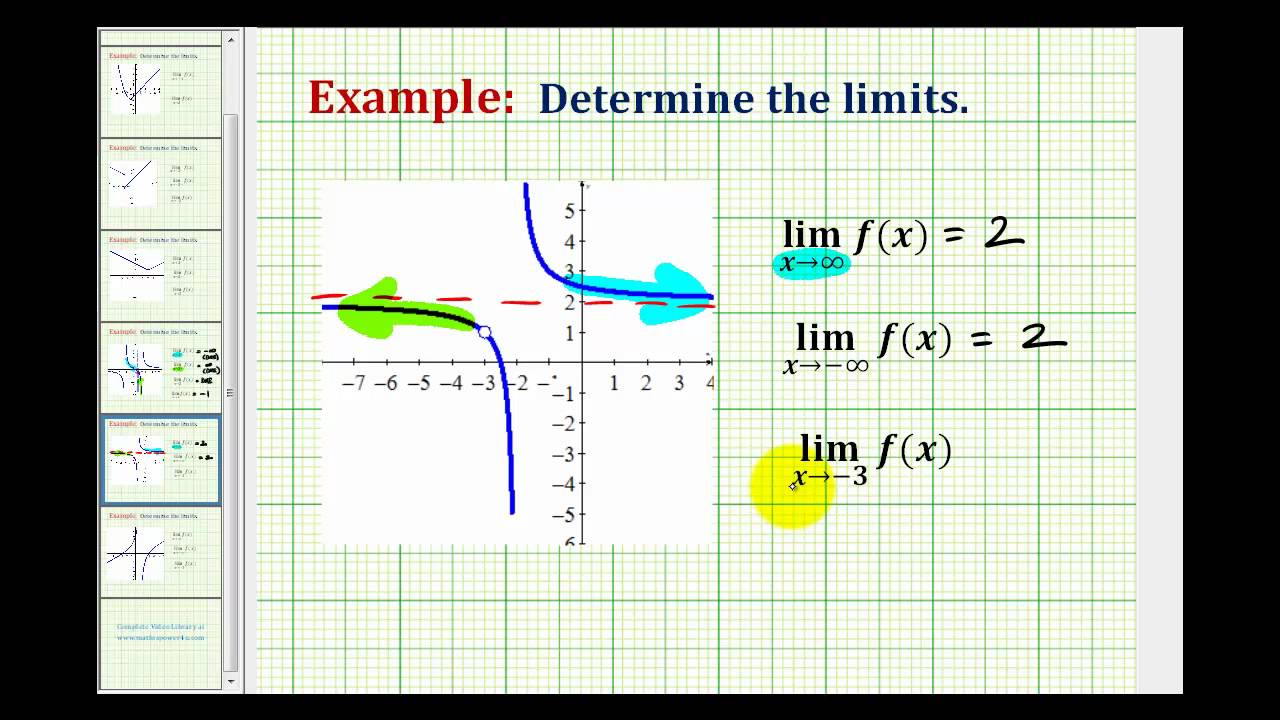



Examples Determining Limits At Infinity Graphically Youtube



1 4 Limits At Infinity And Horizontal Asymptotes End Behavior Mathematics Libretexts
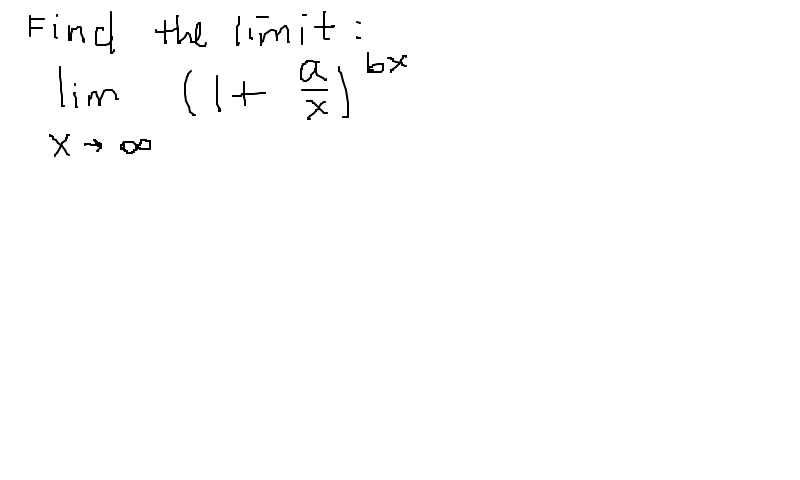



What Is The Limit As X Approaches Infinity Of 1 A X Bx Socratic




Limits At Infinity Infinite Limits And Asymptotes



Question Video Graphing Using Derivatives Of Given Functions Nagwa




Finding The Limit Free Math Help



Finding Limits Graphically



2 5 Limits At Infinity Mathematics Libretexts




Limits At Infinity Infinite Limits And Asymptotes




What S The Limit When X Approaches 1 Socratic
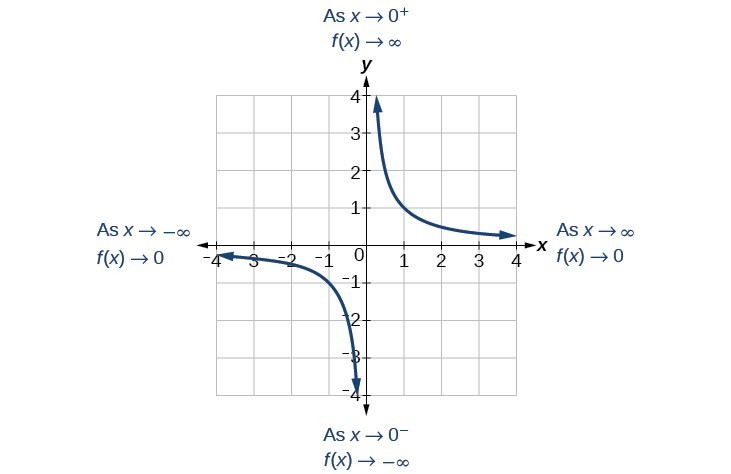



Use Arrow Notation College Algebra




Why Is Limit Of This Function Infinity As X Approaches Infinity Mathematics Stack Exchange



Infinity And Dne In Limits




Given The Function F X 6x 3 2x 2 The Chegg Com
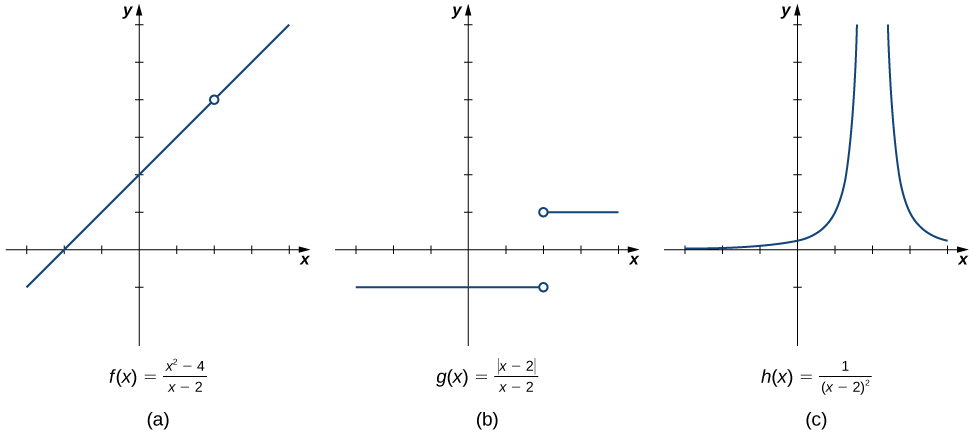



2 2 The Limit Of A Function Calculus Volume 1



Www Swl K12 Oh Us Downloads 3 5 limits at infinity Pdf




Limits



Formal Definition Of The Limit
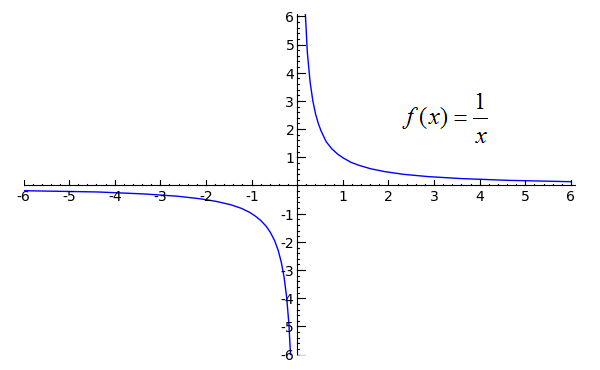



Sage Calculus Tutorial One Sided Limits



What Is The Value Of Limit Of E X X As X Approaches Infinity Quora




Calculus How Is The Answer To Lim X Pi 2 Tan X Negative Infinity And Positive Infinity Quora



Q Tbn And9gcsazoostrpnrtf4rizmcmms5l1qte8refyfv4dl3jsntkt60xol Usqp Cau




Limit As X Approaches Infinity For Log Of Greatest Integer Over X Youtube




Limits
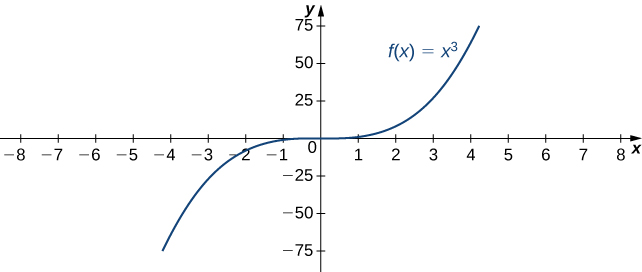



1 4 Limits At Infinity And Horizontal Asymptotes End Behavior Mathematics Libretexts
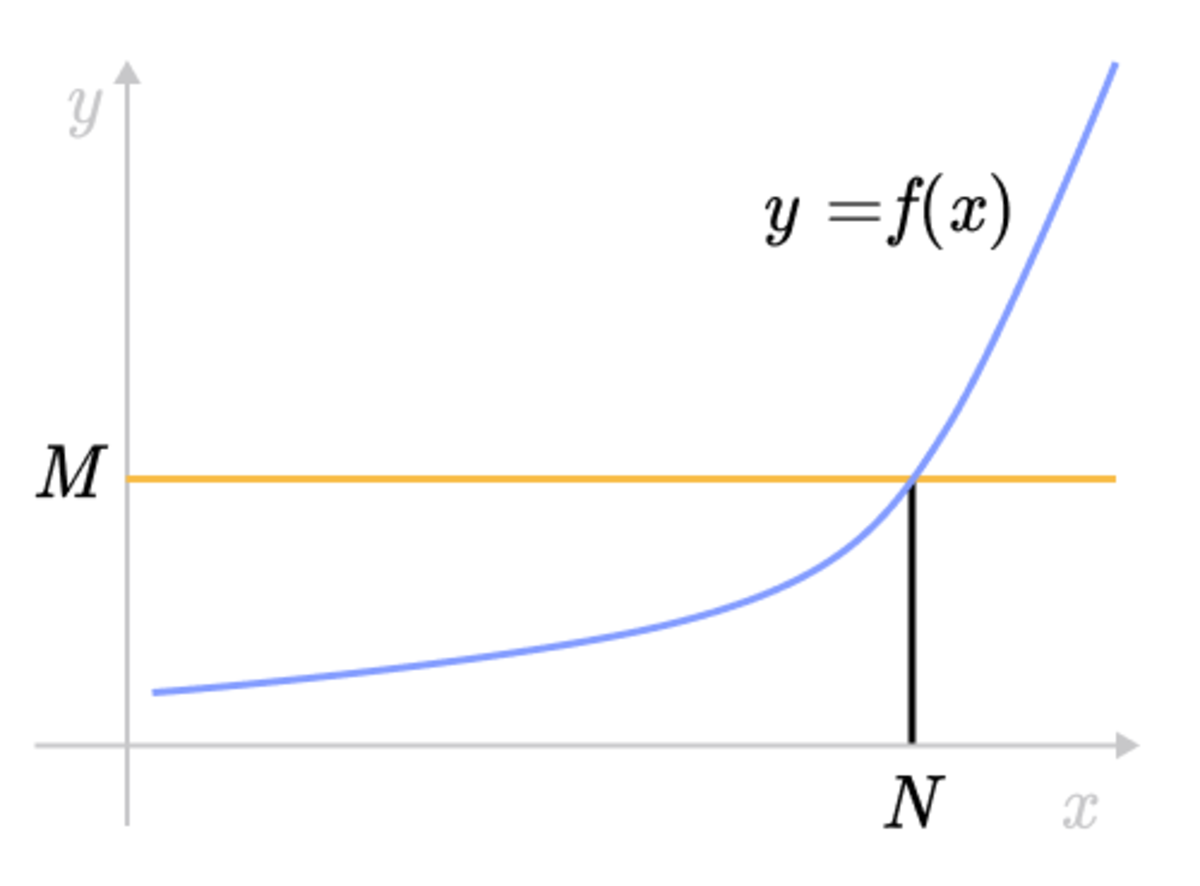



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki




How To Find Limits Using Asymptotes Video Lesson Transcript Study Com
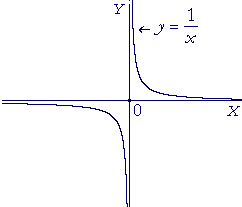



The Limit Infinity An Approach To Calculus




On Infinite Limits Mathematics Stack Exchange



Infinite Limits And Vertical Asymptotes Calculus Socratic




Limits




Calculus First Day More Basic Limits That You May Encounter



1
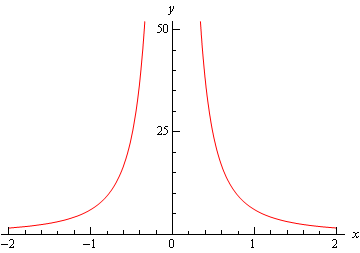



Calculus I Infinite Limits



Calculus Limit Function Take The Limit As X Approaches



Solving Limits At Infinity Intuition And Examples




Use The Information To Sketch A Graph Of F X A Limit As X Approaches Infinity Of F X 1 B Limit As X Approaches 2 Of F X Infinity C Limit As
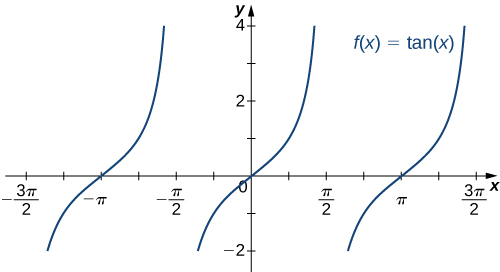



2 5 Limits At Infinity Mathematics Libretexts



Solving Limits At Infinity Intuition And Examples




Limits
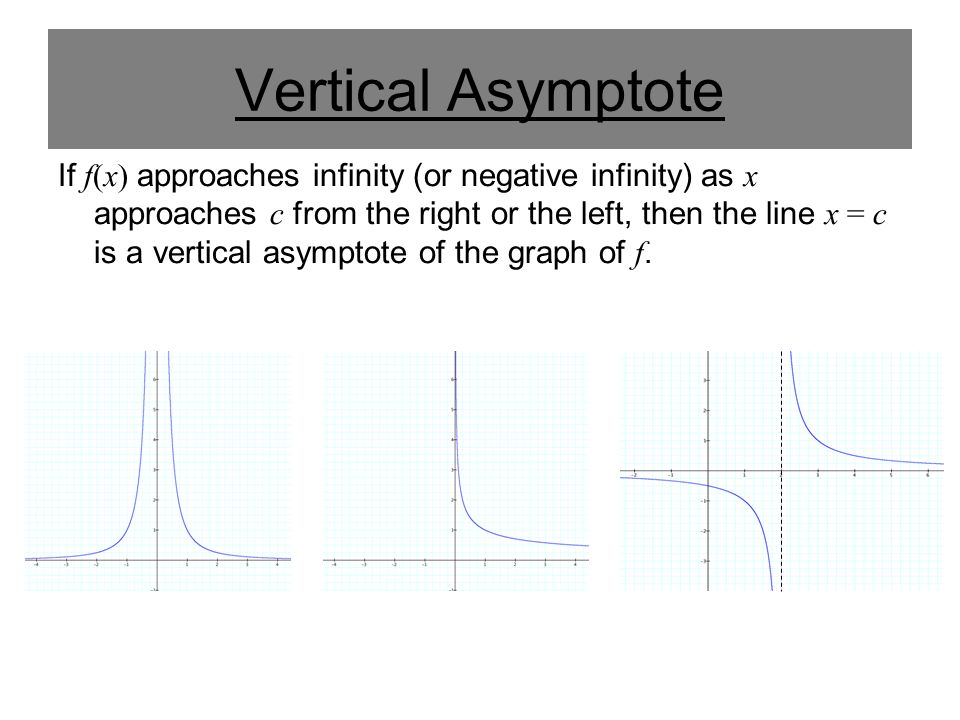



Section 1 5 Infinite Limits Ppt Download
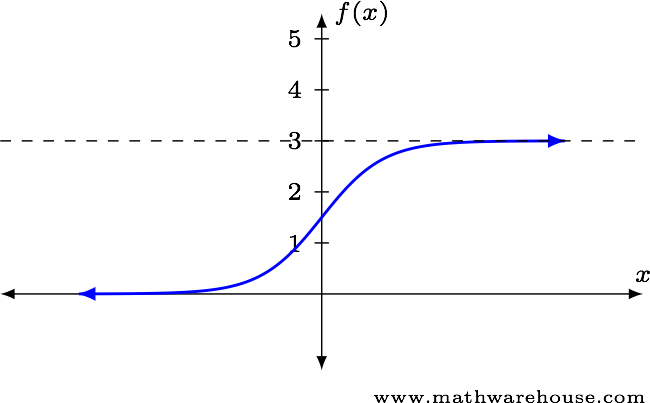



Limits At Infinity Concept How To Solve With Examples



Q Tbn And9gcsazoostrpnrtf4rizmcmms5l1qte8refyfv4dl3jsntkt60xol Usqp Cau




Limits



Limit Of Function Continuous Function Limit At Infinity
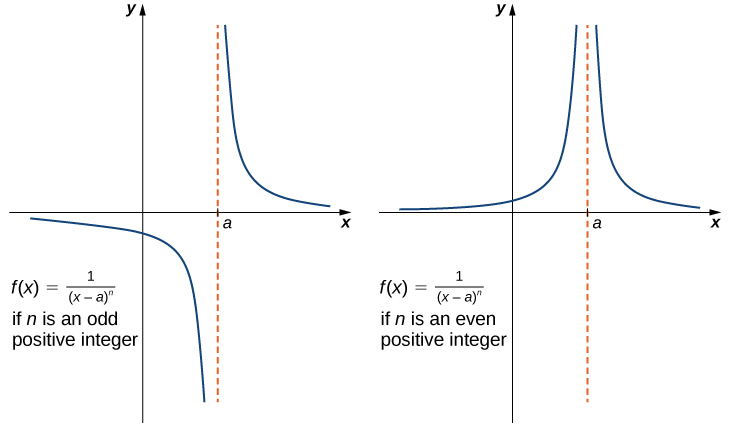



2 2 The Limit Of A Function Calculus Volume 1




Question 37 For The Function F X Use A Graphing Chegg Com
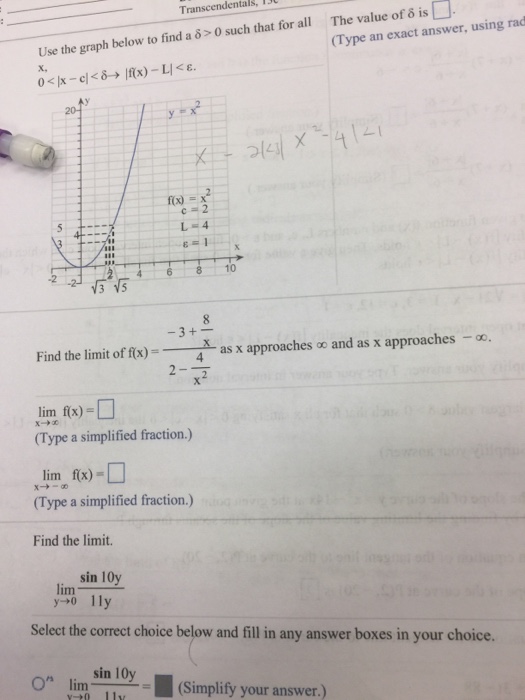



Find The Limit Of F X 3 8 X 2 4 X 2 As X Chegg Com




Find Limit Of X 2 E X As X Approaches Infinity Mathematics Stack Exchange



1 Limits And Differentiation
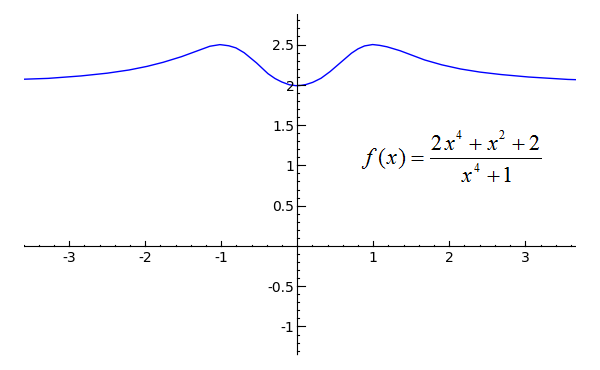



Sage Calculus Tutorial Limits At Infinity




Question Video Finding The Limit Of A Composition Of Rational Functions At Infinity Nagwa




Introduction To Limits At Infinity Video Khan Academy
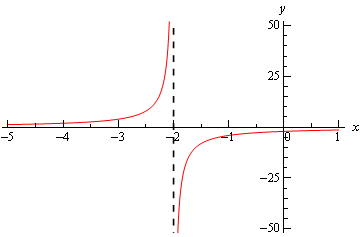



Calculus I Infinite Limits
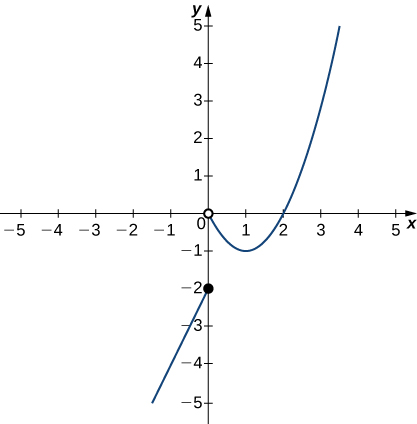



2 2 The Limit Of A Function Calculus Volume 1




Limits




End Behavior Of Functions Ck 12 Foundation
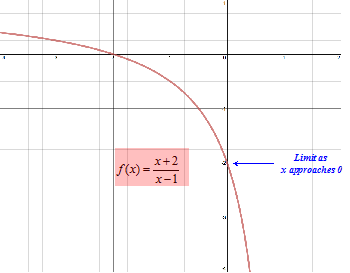



Limits Introduction And One Sided Limits




Limits At Infinity Infinite Limits And Asymptotes
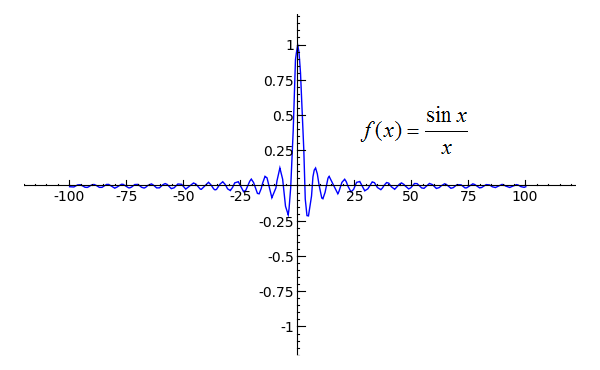



Sage Calculus Tutorial Limits At Infinity
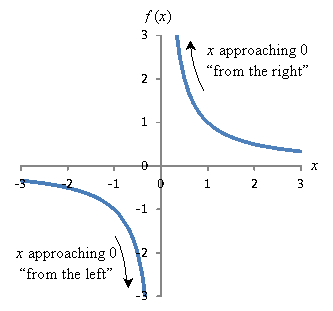



Precalculus How To Calculate Limits For Various Functions Universalclass
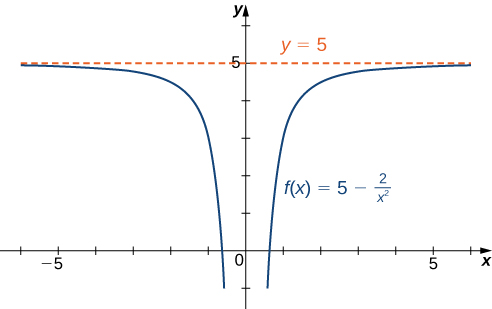



4 6 Limits At Infinity And Asymptotes Calculus Volume 1




2nd Hour Honors Pre Calculus B Spring 13 13




Limits At Infinity Of Quotients Part 1 Video Khan Academy



Finding Limits Graphically



Calculus Limit Function Take The Limit As X Approaches




Connecting Limits At Infinity Notation And Graph Video Khan Academy



1
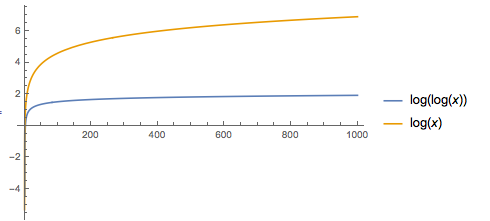



How Do You Find The Limit Of Ln X 1 X As X Approaches Infinity Socratic




2 6 Limits At Infinity X X As X Approaches Infinity F X As X Gets Larger And Larger F X As X Gets Larger And Larger In The Negative Direction Ppt Download



Finding Limits Algebraically



Www Swl K12 Oh Us Downloads 3 5 limits at infinity Pdf




How Can E X Seemingly Approach 0 As X Approaches Negative Infinity Mathematics Stack Exchange



0 件のコメント:
コメントを投稿