Free tangent line calculator find the equation of the tangent line given a point or the intercept stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyDec 27, 19 · \(\cos 2X = \frac{\cos ^{2}X – \sin ^{2}X}{\cos ^{2}X \sin ^{2}X} Since, cos ^{2}X \sin ^{2}X = 1 \) Dividing both numerator and denominator by \(\cos ^{2}\)X, we get \(\cos 2X = \frac{1\tan ^{2}X}{1\tan ^{2}X} Since, \tan X = \frac{\sin X}{\cos X} \)Observe that by taking the substitution \(u=\cos x\) in the last example, we ended up with an even power of sine from which we can use the formula \(\sin^2x\cos^2x=1\) to replace any

Analytic Trig Ppt Video Online Download
Tan 2x formula in terms of tan
Tan 2x formula in terms of tan-Formula cos 2 θ = 1 − tan 2 θ 1 tan 2 θ A mathematical identity that expresses the expansion of cosine of double angle in terms of tan squared of angle is called the cosine of double angle identity in tangentThe intuitive notion that a tangent line "touches" a curve can be made more explicit by considering the sequence of straight lines (secant lines) passing through two points, A and B, those that lie on the function curveThe tangent at A is the limit when point B approximates or tends to AThe existence and uniqueness of the tangent line depends on a certain type of mathematical



Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples
Tan (AB) = tanA tanB / 1 tanA×tanBThe hyperbolic tangent function is an old mathematical function It was first used in the work by L'Abbe Sauri (1774) This function is easily defined as the ratio between the hyperbolic sine and the cosine functions (or expanded, as the ratio of the half‐difference and half‐sum of two exponential functions in the points and )The effect of \(p\) on the tangent function is a horizontal shift (or phase shift);
Tan(3x) in terms of tan(x), write tan(3x) in terms of tan(x), using the angle sum formula and the double angle formulas, simplifying trig identities, trigonoSep 14, 10 · therefore, texsin(x)=\frac{tan(x)}{\sqrt{1tan^2(x)}}/tex But I graphed this and it only looks right half of the time What I should have is the plus or minus when taking the root of cos 2 (x) but I need the plus half the time, and the minus the other half of the time and then merge them to describe sin(x) in terms of tan(x)3 The formula cos2A = cos2 A−sin2 A We now examine this formula more closely We know from an important trigonometric identity that cos2 Asin2 A = 1 so that by rearrangement sin2 A = 1− cos2 A So using this result we can replace the term sin2 A in the double angle formula This gives
We will learn how to express the multiple angle of cos 2A in terms of tan A Trigonometric function of cos 2A in terms of tan A is also known as one of the double angle formula We know if A is a number or angle then we have, cos 2A = cos 2 A sin 2 A cos 2A = \(\frac{cos^{2} A sin^{2} A}{cos^{2} A}\) ∙ cos 2 A ⇒ cos 2A = cos 2 A (1Sep 19, 18 · Example \(\PageIndex{1}\) Integrating powers of sine and cosine Evaluate \(\int\sin^5x\cos^8x\ dx\) Solution The power of the sine term is odd, so we rewrite \(\sin^5x\) asMar 10, 17 · The formula given in my book does not seem to work in Mathcad Prime 30 In the book there is no multiplier (*) printed after tan^2 and cos^2 There is just empty space I did change the formula around in all kinds of ways I put tan inside parenthesis like (tan)^2, or (tan^2*(gammaQ)), or (tan(gammaQ)^2) but nothing works What do I do wrong?
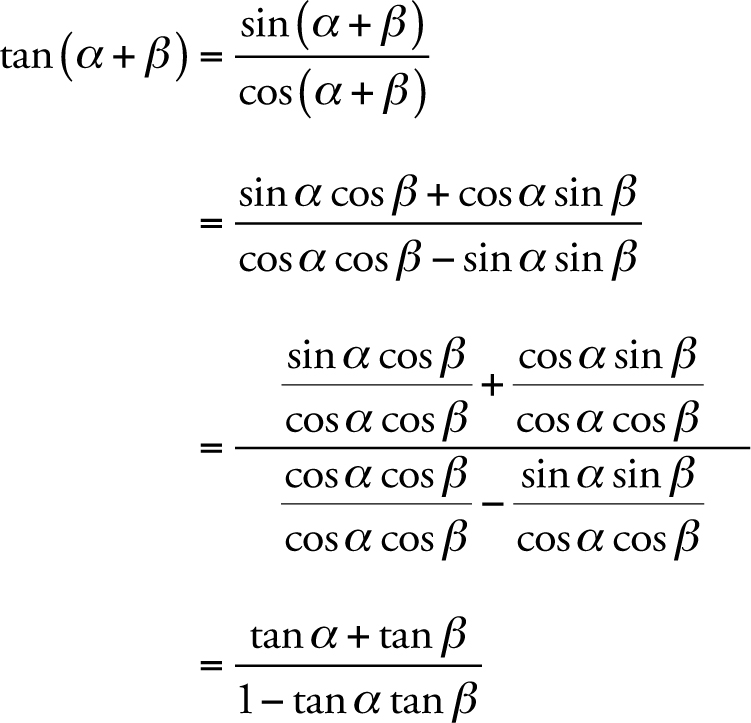


Tangent Identities



7 Techniques Of Integration Techniques Of Integration 7
X Therefore, tan 2 x = ( sin 2 x / 1 − 2 sin 2 x) Is it possible to do it in terms of cosFrom this formula we can derive tan(2x) as tan(xx) So tan(2x)= 2tanx/1tanxtanx We can always go for the longer approch from sinx/cosx to derive this formulaIntroduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes



Solved Section 7 3 Double Angle Half Angle And Product Chegg Com



Rewrite Sin 2x Tan 2x In Terms Of The First Power Of Cosine Using The Power Reducing Formula Study Com
Jan 30, 07 · Homework Statement seems simple, but i am stumped Says write cos(x) in terms of tan(x) Homework Equations would this be a reciprocal equation?I'm lost The Attempt at a Solution i dont even know where to beginOct 18, 18 · If j is even and j ≥ 2, rewrite secjx = secj − 2xsec2x and use sec2x = tan2x 1 to rewrite secj − 2x in terms of tanx Let u = tanx and du = sec2x 2 If k is odd and j ≥ 1, rewrite tankxsecjx = tank − 1xsecj − 1xsecxtanx and use tan2x = sec2x − 1 to rewrite tank − 1x in terms



Math34 Trigonometric Formulas



Lim X Pi 4 Tanx Tan2x
If the function is a sum, product, or quotient of basic functions, use the appropriate rule to determine its derivative \(\displaystyle h(x) = \tan(2^x)\) \(\displaystyle p(x) = 2^x \tan(x)\) \(\displaystyle r(x) = (\tan(x))^2\) \(\displaystyle m(x) = e^{\tan(x)}\) \(\displaystyle w(x) = \sqrt{x} \tan(x)\) \(\displaystyle z(x) = \sqrt{\tan(x)}\)Cos 2x = (1tan^2 x)/(1 tan^2 x)` Plugging `tan x = sqrt6/3` in the formulas above yieldsFind a numerical value of one trigonometric function of x for csc x=sin x tan x cosx D cotx=1 Find sec x if tan^2x=1/2 D Given 1tanx/1cotx=2, find a numerical value of one trigonometric function of x B tanx=2 Write an expression for the power in terms of A


C3 Trig The Student Room



Solve The Following Equation Tan X Tan 2x Tan 3x 0
Dec 09, 15 · Get an answer for '`tan^4(2x)` Use the power reducing formulas to rewrite the expression in terms of the first power of the cosine' and find homework help for other Math questions at eNotesThe arctangent of x is defined as the inverse tangent function of x when x is real (x ∈ℝ) When the tangent of y is equal to x tan y = x Then the arctangent of x is equal to the inverse tangent function of x, which is equal to y arctan x= tan1 x = y Example arctan 1 = tan1 1 = π/4 rad = 45° Graph of arctan Arctan rulesApr 05, 21 · tan^2x sin^2x = (sin^2 x) (sin^2 x)/cos^2x = (1cos^2 x) (1 cos^2 x)/cos^2 x = (1 2cos^2 x cos^4 x)/cos^2x = 1/cos^2 x 2 cos^2 x now remember that cos (2A) = 2cos^2 A 1 which leads to cos^2 A = (cos (2A) 1)/2 so above = 2/ (cos (2x) 1) 2 (cos (2x) 1)/2



Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
Aug 18, 11 · cos(2A) = 2cos²A – 1 So cos(2A) = cos²A sin²A = 1 – 2sin²A = 2cos²A – 1 Finally, all we need to do now is derive the tangent double angle formula Like the previous examples, change the B's to A's in the addition formula for tangentApr 07, 16 · I know $$ \cos(z) = \frac{e^{iz} e^{iz}}{2} , \hspace{2mm} \sin(z) = \frac{e^{iz} e^{iz}}{2i}, $$where $$ \tan(z) = \frac{\sin(z)}{\cos(z)} $$Applying the above, with a little manipulation, gives me$$ \tan(z) = \frac{i\left(e^{iz} e^{iz}\right)}{e^{iz} e^{iz}}$$Sep 16, 07 · tan (2 x 225)= 2tan (225)/ 1 tan²225 tan 45 1 tan²225 = 2tan 225 1 tan²225 = 2tan 225 Let x = tan 225 1 x² = 2x x² 2x 1 = 0 x = 2 ± √ (8)/2 x = 1 ± √ (2) but x = tan 225 > 0, so we take the positive root



How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



7 2 Trigonometric Integrals Ppt Download
Oct 18, 16 · 1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 weIf the power of the secant \(n\) is odd, and the power of the tangent \(m\) is even, then the tangent is expressed in terms of the secant using the identity \(1 {\tan ^2}x \) \(= {\sec ^2}x\) After this substitution, you can calculate the integrals of the secantThe sum of two angles is written as a b in mathematics It is actually a compound angle The tangent of a compound angle a plus b is expressed as tan ( a b) mathematically The tan of the sum of angles a and b is equal to the quotient of the sum of the tangents of angles a and b by the subtraction of the product of tangents of angles a and b from one


Tan2x ただの悪魔の画像



If Tan X Y 3 4 Tan X Y 5 12 What S Tan2x Quora
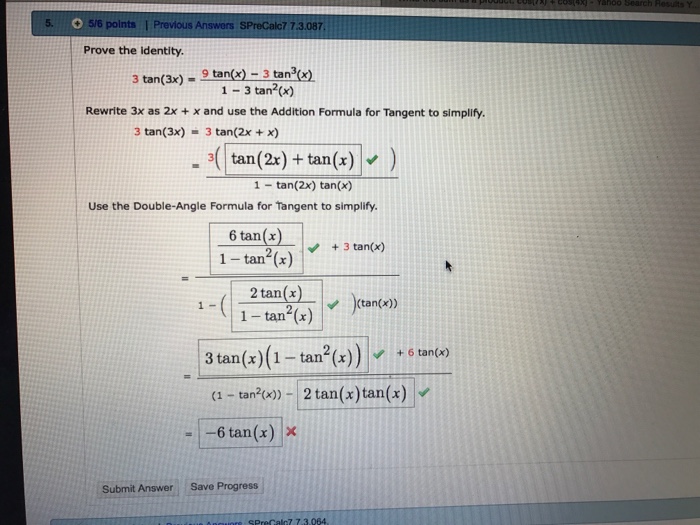
Prove the identity 3 tan(3x) = 9 tan (x) 3 tan^3 (x)/1 3 tan^2 (x) Rewrite 3x as 2x x and use the Addition Formula for Tangent to simplifyFeb 22, 21 · Tan2x Formulas Tan2x Formula = 2 tan x 1 − t a n 2 x We know that tan (x) = sin (x)/cos (x)About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
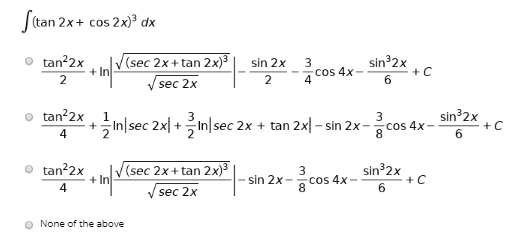


Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby



Sec22x 1 Tan 2x Find The General Solution Maths Trigonometric Functions Meritnation Com
The formula of tan3a is the ratio of 3TANATAN ^3A – 1TAN^2ATHIS IS ONLY FROM THE KNOWN AND TRUTHFOR MORE DETAILS AND PROOVES AGAIN ASKGraph y=tan(2x) Find the asymptotes Tap for more steps For any , vertical asymptotes occur at , where is an integer The trig function can be graphed using the amplitude, period, phase shift, vertical shift, and the points Vertical Asymptotes where is an integer Amplitude NoneYou need to write sin 2x and cos 2x in terms of tanx such that `sin 2x = (2 tan x)/(1 tan^2 x);



Cosx 3 5 Find Tanx 2 Half Angle Tangent Formula Derivation With Important Example Youtube



Solved Problem 4 Using The Sin And Cos Addition Formulas Chegg Com
Aug 28, · 2 tan1 x = sin1 (2x/(1x 2)), x ≤ 1 16 2tan1 x = cos1 ((1x 2)/(1x 2)), x ≥ 0 17 2tan1 x = tan1 (2x/(1x 2)), 1Dec , 16 · equation 50and put B = A to get tan(A A), or use equation 59for sin 2A / cos 2nd divide top and bottom by cos² A Either way, you get (60)tan 2A= 2 tan A/ (1 − tan² A)The entire graph slides to the left or to the right For \(p > 0\), the graph of the tangent function shifts to the left by \(p\) For \(p < 0\), the graph of the tangent function shifts to the right by \(p\)



How Many Can You Derive From First Principles Ppt Download



Solved Use The Power Reducing Formulas To Rewrite Tan 2x Chegg Com
Feb 12, · Ex 33, 23 Prove that tan4𝑥 = (4 tan〖𝑥 (1−tan2𝑥)〗)/(1 − 6 tan2 𝑥tan4 𝑥) Taking LHS tan 4x We know that tan 2x = (2 𝑡𝑎𝑛𝑥)/(1 − 𝑡𝑎𝑛2 𝑥) Replacing x with 2x tan (2 × 2x) = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) tan 4x = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) = (2 taSince both terms are perfect squares, factor using the difference of squares formula, where and Apply the tangent double angle identity Simplify the denominatorCalculus questions and answers (21 3 Consider the function (x) = tan(2x (5 marks) a Determine f '(x) b Determine the slope of the tangent to the curve f(x) at the point with xcoordinate 37 4 c Determine the equation of the tangent to


How To Write Sin X In Terms Of Tan X Quora



Maclaurin Series Tan X
May 10, 21 · The several cos 2 x \cos 2x cos 2 x definitions can be derived by using the Pythagorean theorem and tan x = sin x cos x \tan x = \frac{\sin x}{\cos x} tan x = cos x sin x Double Angle FormulasEven though each trigonometry function is perfectly wonderful, being able to express each trig function in terms of one of the other five trig functions is frequently to your advantage For example, you may have some sine terms in an expression that you want to express in terms of tangent, so that all the functionsSin 2 ( x ) cos 2 ( x ) = 1 1 tan 2 ( x ) = sec 2 ( x ) 1 cot 2 ( x ) = csc 2 ( x ) There are also the reciprocal identities sin ( x ) = 1 csc ( x ) cos ( x And the producttosum formulas sin



Answered Power Reducing Formulas Cos 2x 1 Cos Bartleby



Tan2x Formula In Terms Of Tan Edurev Class 12 Question
Dec 08, 16 · Transcript Example 14 Show that tan 3 tan 2 tan = tan 3 tan 2 tan We know that 3 = 2 Therefe, tan 3 = tan (2 ) tan 3 = tan 2 tan 1 tan 2 tan tan 3 tan 3 tan 2Halfangle formula for , however, we have Notice that we mentally made the substitution when integrating Another terms of tangent using the identity We can then evaluate the integral by substituting with 1 7 tan 7x 1 9 tan 9x C u7 7 u9 9 C tan2x 2 ln sec x C y tan x sec2x dx y tan x dx y tan x sec 2x 1 dx y tan3x dx y tan x tan2x



Trig Identity Sec2x Minus Tan2x T10 Youtube



Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55



Solved Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities



How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



Solve Tan2x Cot X P 3 Brainly In



Solve Sinxtanx 1 Tanx Sinx


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities



How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



Tan 2x Formula Learn Formula For Calculating The Double Angle Tan 2x


Analytic Trigonometry



How To Solve Tan 1 2x 1 X2 Cot 1 1 X2 2x Pie 3 Brainly In



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2



Limit X Tends 0 X 2 Tan2x Tanx Brainly In


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities


What Is The Formula Of Tan2x Quora


What Is The Proof Of Tan 3x Quora



Ex 3 3 19 Prove Sin X Sin 3x Cos X Cos 3x Tan 2x



Answered Find The Indefinite Integral Sec 2x Bartleby



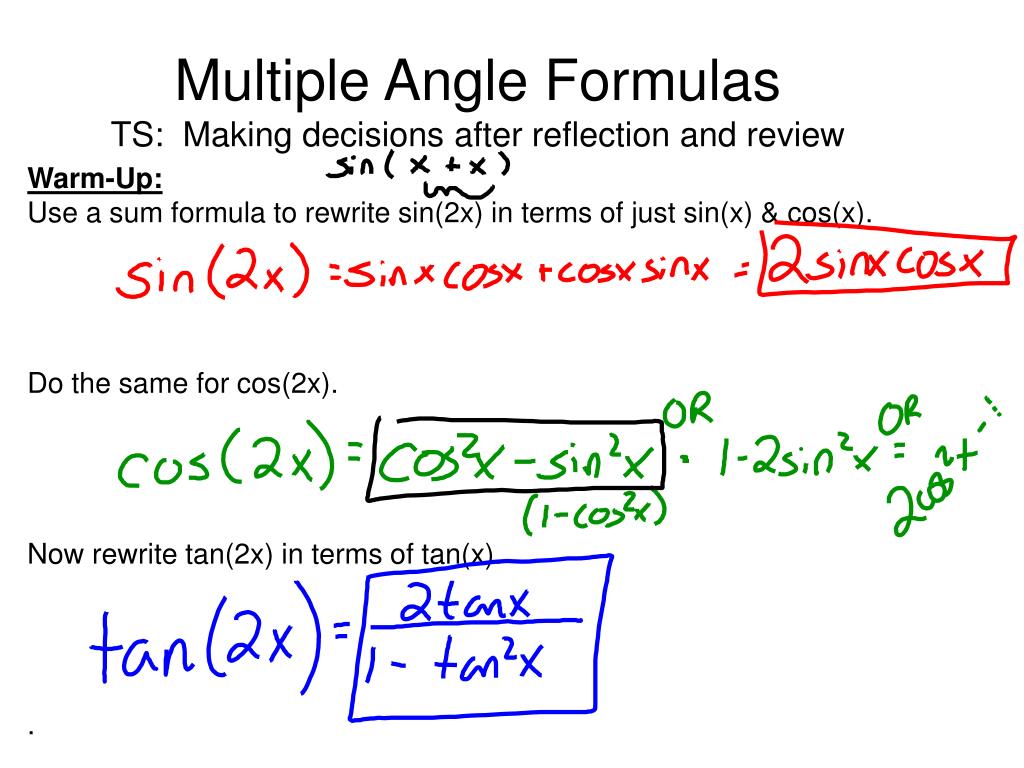
Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download



Analytic Trig Ppt Video Online Download



How To Take The Derivative Of Tan X Video Lesson Transcript Study Com



Solve Tan2x Cot X P 3 Brainly In


What Is The General Solution Of X For Tan X Tan2x 1 Quora


What Is The Formula Of Tan2x Quora



Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x


Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id


Prove Sin2x 2tanx 1 Tan 2x Socratic



Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x



Write Cos2x In Terms Of Tanx Double Angle Transformation Youtube



If Cos 2x Cos 4x 1 Then Tan 2x Tan



Section 7 3 Double Angle And Half Angle Formulas Flashcards Quizlet


Tan2x ただの悪魔の画像


Find The General Solution By The Method Of Variation Of Parameters Y 4y Tan 2x Sarthaks Econnect Largest Online Education Community


Trig Find Tan X Given Tan 2x 2 Pi X 3pi 2 Cheatatmathhomework



Weierstrass Substitution Wikipedia
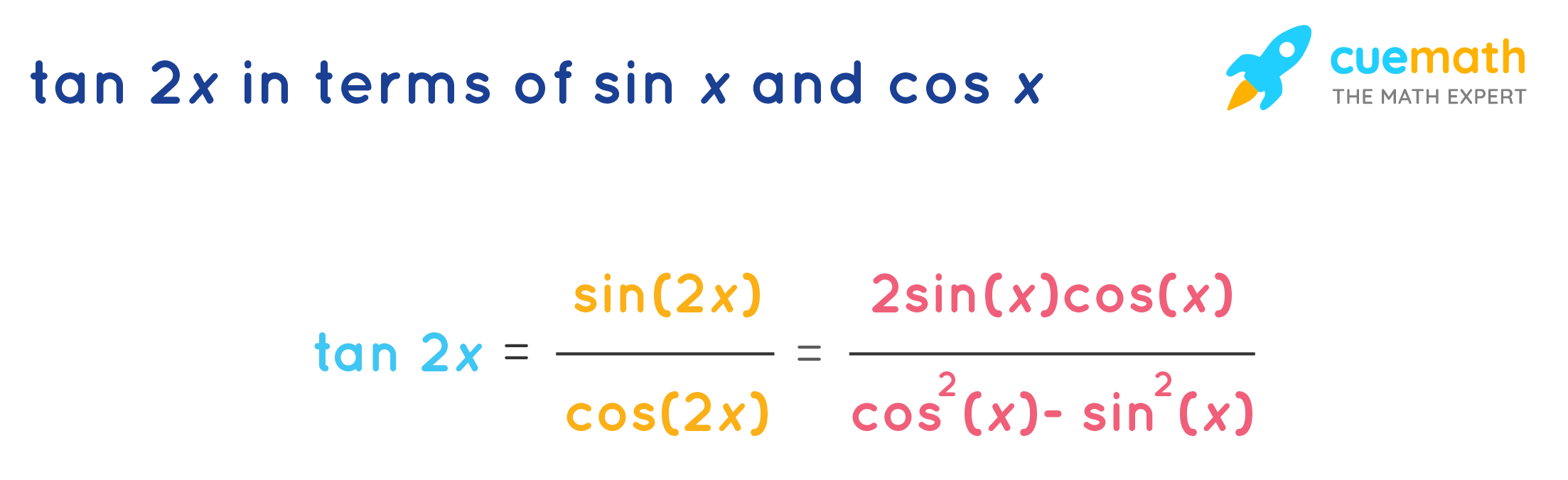


Tan 2x Formula Learn Formula For Calculating The Double Angle Tan 2x



Tangent Half Angle Formula Wikipedia



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Inf Chegg Com


A Trig Identity
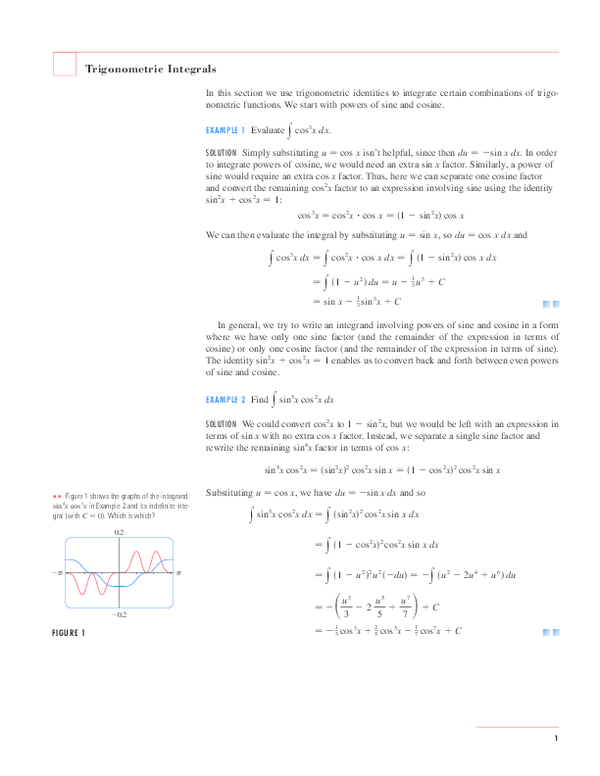


Pdf Trigonometric Integrals Jerome Delen Academia Edu



4 Tan 2x 2 Sec 2x 1 0 X In



Tangent Half Angle Formula Wikipedia



Inttanx Tan2x Tan3x Dx Is Equal To


Differentiate The Following From First Principles I Tan 2 X Ii Tan 2x 1 Sarthaks Econnect Largest Online Education Community



Solved Prove The Identity 3 Tan 3x 9 Tan X 3 Tanx 13 Chegg Com



Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction
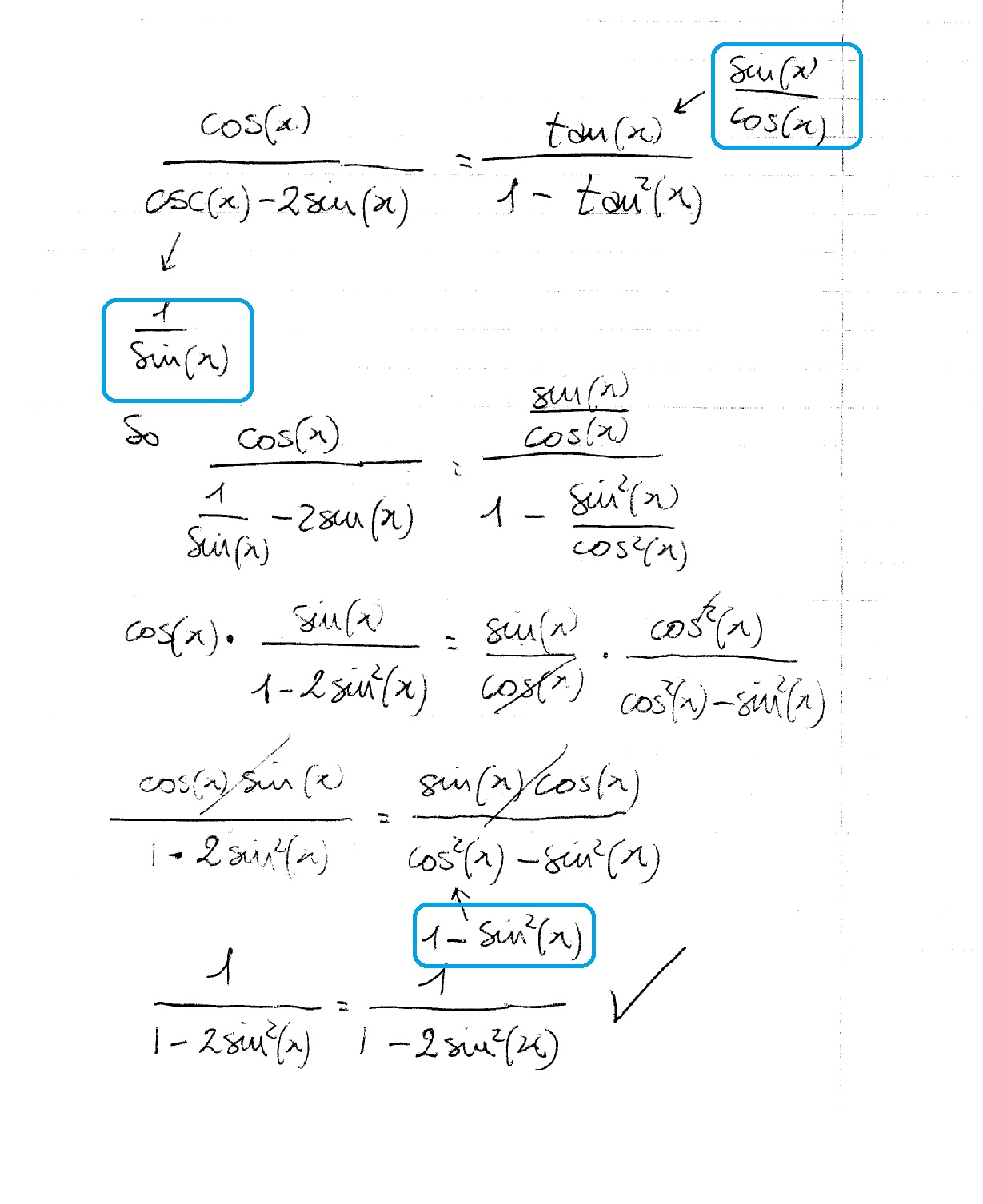


How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic


Sin 2x Cos 2x And Tan 2x



Lim X 0 Log Tan 2x Tan 2 2x



Math34 Trigonometric Formulas



How To Write Tan 3x In Terms Of Tan X Youtube
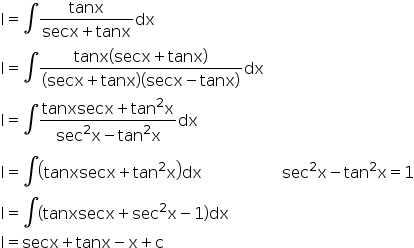


Evaluate Integration Tanx Sec X Tan X Dx Explain In Great Detail Mathematics Topperlearning Com Cbuy1yhh


What Is The Formula Of Tan2x Quora



Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube



Section 7 3 Double Angle Half Angle And Sum



Integrate Tan 2x By Parts
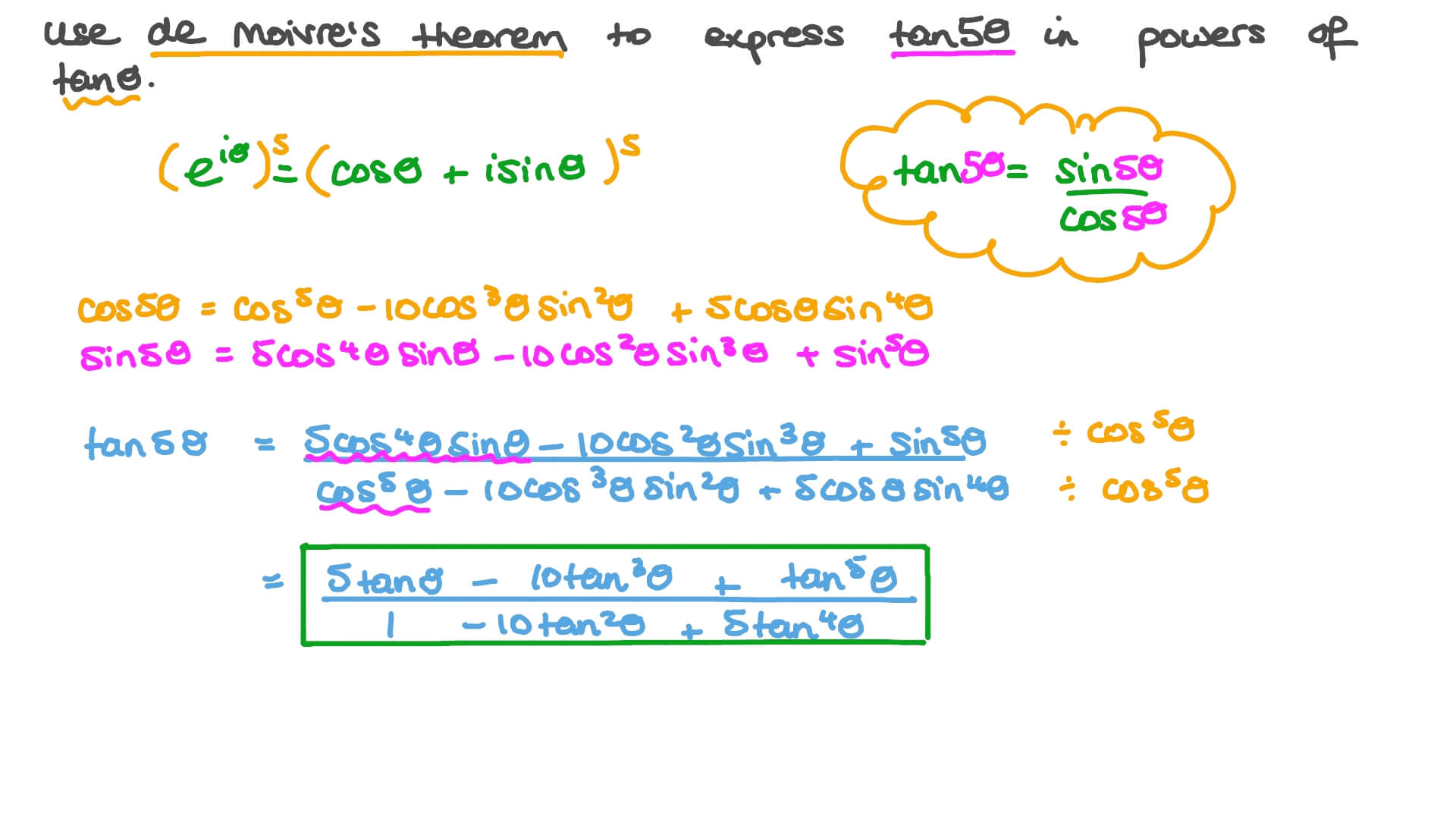


Question Video Using De Moivre S Theorem To Derive Trigonometric Identities Nagwa
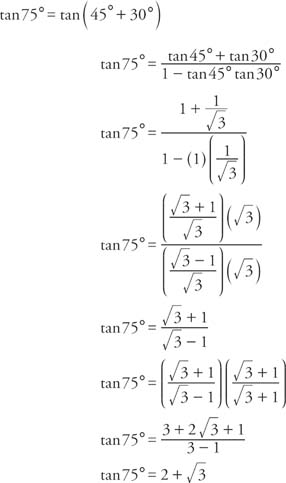


Tangent Identities


What Is The Formula Of Tan2x Quora



Maclaurin Series Tan X



Rd Sharma Solutions For Class 11 Chapter 11 Trigonometric Equations Download Free Pdf


Solved Prove The Identity 3 Tan 3x 9 Tan X 3 Tan Chegg Com



In This Solution Why The 2 Tan2x 1 Tan 2x Was Dived By1 2tan 2x 1 Tan 2x 2 Trigonometric Functions Q23 Prove That Solution 4tanx La Tan X Maths Trigonometric Functions Meritnation Com



Tangent Half Angle Formula Wikipedia



Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube



Prove That Tan4x 4tanx 1 Tan 2x 1 6tan 2x Tan 4x



Sin2x Formula In Terms Of Tan How Do You Write Tan 2x In Terms Of Sinx



Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
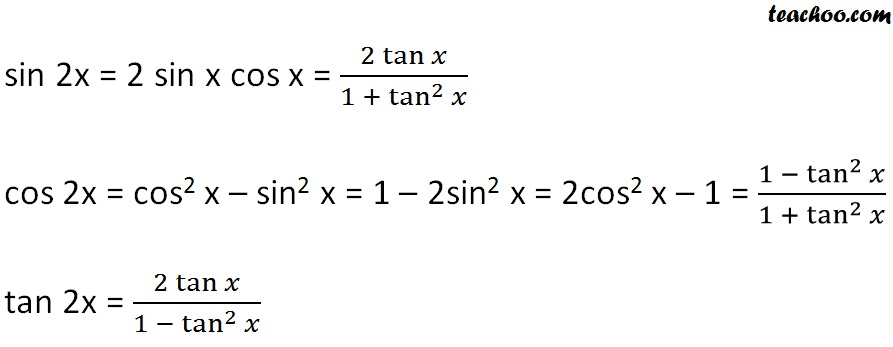


Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
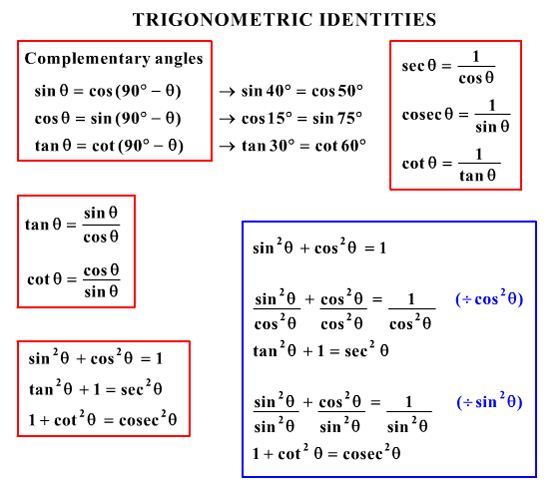


How To Solve Tan 2y Sec 2y Tan 4y Tan 2y Socratic


Is Tan 2x Equal To Tan X 2



Power Reducing Formulas And How To Use Them With Examples Owlcation



0 件のコメント:
コメントを投稿